
Integrating curvatures over beam length, the deflection, at some point along x-axis, should also be reversely proportional to I. Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the developed curvature is reversely proportional to the moment of inertia I. Where Ixy is the product of inertia, relative to centroidal axes x,y, and Ixy' is the product of inertia, relative to axes that are parallel to centroidal x,y ones, having offsets from them d_. Indeed, the rotational inertia of an object. Rotational inertia plays a similar role in rotational mechanics to mass in linear mechanics. There is Second moment of area calculator t beam that can make the technique.


#2ND MOMENT OF INERTIA CALCULATOR HOW TO#
How to Calculate Moment of Inertia MOI Calculation. It is a scalar value which tells us how difficult it is to change the rotational velocity of the object around a given rotational axis. Second Moment of Area Formula: Symbol, Equation Area moment of inertia. It should not be confused with the second moment of area, which is used in bending calculations. The general formula of torsional stiffness of bars of non-circular section are as shown below the factor J is dependent of. In this video we introduce the second moment of area / inertia and its significance in the behaviour of a structure, learning how to determine the second mom. Where I' is the moment of inertia in respect to an arbitrary axis, I the moment of inertia in respect to a centroidal axis, parallel to the first one, d the distance between the two parallel axes and A the area of the shape (=bh in case of a rectangle).įor the product of inertia Ixy, the parallel axes theorem takes a similar form: The second moment of area for the entire shape is the sum of the second moment of areas of all of its parts about a common axis. Rotational inertia is a property of any object which can be rotated. The so-called Parallel Axes Theorem is given by the following equation: We generally assume that the 'width of any shape' is the length of each side along the horizontal x-axis. We can differentiate between the moment inertia at the horizontal x-axis (denoted Ix), as well as the moment inertia at the vertical y-axis. Rajput) The strength of a beam is dependent on the section modulus (Z) and is of greater.
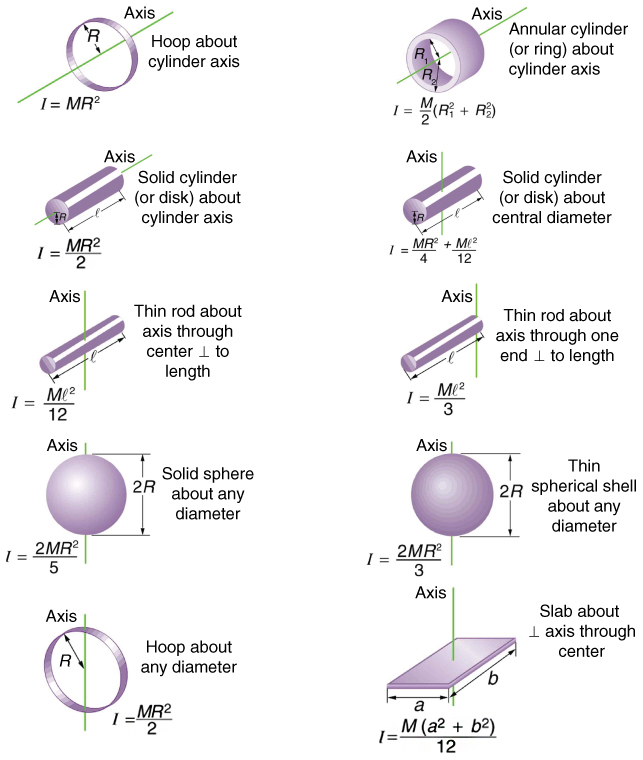
The moment of inertia of any shape, in respect to an arbitrary, non centroidal axis, can be found if its moment of inertia in respect to a centroidal axis, parallel to the first one, is known. The units of area moment-of-inertia are meters to a fourth power (m4). formula of second moment of areaSection modulus calculator.


 0 kommentar(er)
0 kommentar(er)
